"I only hope that we never lose sight of one thing: that it was all started by a [drawing of a] mouse." - W. Disney #ItsUhTheStuffThatDreamsAreMadeOf
A. OnShape
1) The
first link in a 6D robot arm (Aug 2023)
2) A 2D robot arm (Aug 2023) (3D print Dec 2023)
 |
 |
 |
 |
|
 |
|
|
|
|
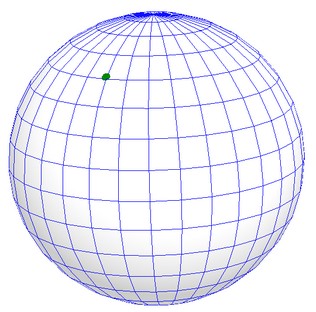
| \(\mathbb{R}P^2\) Boy's Surface (Euler Characteristic) \(\chi = 1\) Non-Orientable 1 \(\mathbb{R}P^2\) (If \(M = \#_{i=1}^g \mathbb{R}P^2\) is the non-orientable connect sum of \(g\) \(\mathbb{R}P^2\)'s, \(\chi(M) = 2-g\). \(g\) is the genus of the surface.) (The Euler characteristic \(\chi\) and orientability/non-orientability of a surface uniquely characterize it up to diffeomorphism.) |
\(S^2\) 2D-Sphere \(\chi\ = 2\) Orientable Orientation Double-Cover of \(\mathbb{R}P^2\) (If 2\(M\) is the double-cover of \(M\), then \(\chi(2M) = 2\chi(M)\).) (The 2-sphere acts as an identity elements for connect sum: \(M \# S^2 = M\).) |
\(K^2\) Klein Bottle \(\chi = 0\) Non-Orientable Connect sum of 2 \(\mathbb{R}P^2\)'s Fundamental Relation 1 (FR1) |
\(T^2_1\) Genus-1 2D-Torus \(\chi=0\) Orientable Orientation Double-Cover of 2 \(\mathbb{R}P^2\)'s = 1 \(T_1^2\) (If \(M = \#_{i=1}^g T_1^2\) is the orientable connect sum of \(g\) \(T^2_1\)'s, \(\chi(M) = 2-2g\). \(g\) is the genus of the surface.) |
Connect
Sum of 3 \(\mathbb{R}P^2\)'s \(\chi = -1\) Non-Orientable Connect Sum of 3 \(\mathbb{R}P^2\)'s = Connect Sum of \(\mathbb{R}P^2\) and \(T^2_1\) Fundamential Relation 2 (FR2) |
\(T^2_2\) Genus-2 2D-Torus \(\chi = -2\) Orientable Orientation Double-Cover of 3 \(\mathbb{R}P^2\)'s = Connect Sum of 2 \(T^2_1\)'s |
Connect
Sum of 4 \(\mathbb{R}P^2\)'s \(\chi = -2\) Non-Orientable Connect Sum of 4 \(\mathbb{R}P^2\)'s = Connect Sum of \(K^2\) and \(T^2_1\) (using FR2 then FR1) |
\(T^2_3\) Genus-3 2D-Torus \(\chi = -4\) Orientable Connect Sum of 3 \(T^2_1\)'s |
Connect
Sum of 5 \(\mathbb{R}P^2\)'s \(\chi = -3\) Non-Orientable Connect Sum of 5 \(\mathbb{R}P^2\)'s = Connect Sum of \(\mathbb{R}P^2\), \(K^2\), and \(T^2_1\) (using FR2 then FR1) = Connect Sum of \(\mathbb{R}P^2\) and 2 \(T^2_1\) (using FR2 twice) |
\(T^2_4\) Genus-4 2D-Torus \(\chi = -6\) Orientable Orientation Double-Cover of 5 \(\mathbb{R}P^2\)'s = Connect Sum of 4 \(T^2_1\)'s |
Work:
I had a full-time co-op for Fall 2023 - Summer 2024 at Copland
Corporation (formerly a division of Emerson)
in Sidney, OH working in Data Science.
I had a full-time internship for Summer 2023 at AngleLock by
Controlled Dynamics in Grafton, WI working in Mechanical
Engineering.
Research Interests: My Ph.D. is in manifold topology under Prof. Craig Guilbault (UWM's Math Department's Chairman). However, I am moving my research interests into an application of manifold topology, specifically optimal geometric control theory (optimal control engineering on manifolds). I have a blog related to my learning experiences in these new areas of STEM (for me), This Week's Finds in Second-Order Ordinary Differential Equations on Manifolds and Geometric Control Theory.
